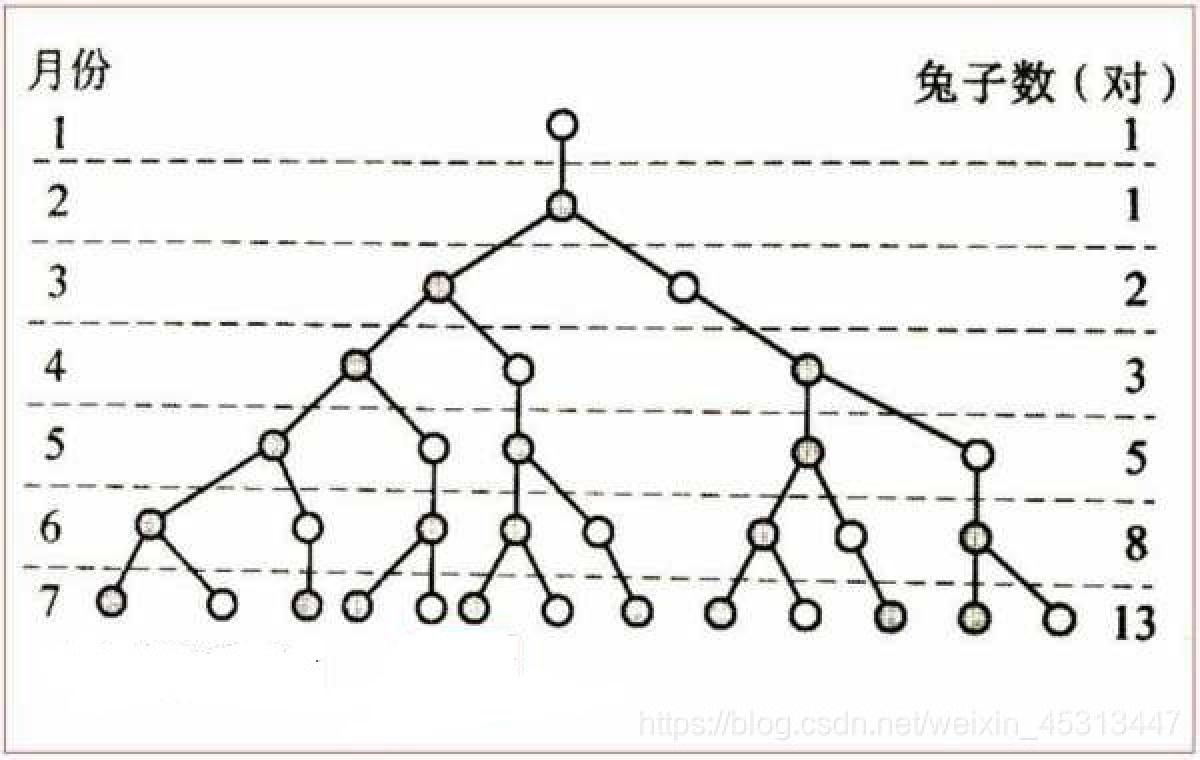
斐波那契数列（Fibonacci sequence），又称黄金分割数列 [1]，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称“兔子数列”，其数值为：1、1、2、3、5、8、13、21、34……在数学上，这一数列以如下递推的方法定z义：F(0)=1，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）。 [2]

意大利数学家莱昂纳多·斐波那契提出的数列。这个数列可以从非常简单的起始条件开始描述：前两个数字是1，接下来的每个数字都是其前两个数字的和。在数学上，这个关系可以递推定义：F(0)=0，F(1)=1，F(n)=F(n - 1)+F(n - 2)，其中n≥2且n为自然数。

斐波那契数列在自然界中普遍存在，艺术、建筑和日常生活中的应用也十分广泛，都在不同程度上反映了这一数学规律。

package main

import "fmt"

func main() {

fmt.Println(fibonacci(8))

fmt.Println(FibArray(8))

fmt.Println(fib(8))

}

// 递归算法

/*使用迭代算法和递归算法都可以实现斐波那契数列，输出数列中的第N项，但是由于递归算法在计算时存在着大

量的重复计算，所以在N值很大时，可能会造成内存的溢出，以及计算时间较长的情况出现，在使用迭代算法

的情况下同样可以实现计算斐波那契数列第N项的功能*/

func FibArray(n int) []int {

arr := make([]int, n)

for i := 0; i < n; i++ {

switch {

case i < 2:

arr[i] = i

default:

arr[i] = arr[i-1] + arr[i-2]

}

}

return arr

}

//迭代算法

/*思路就是当 n <=0 时 return 0，当1 <= n <= 2时 return 1 ，当 n >= 3时，第n项 f(n) =

 f(n-2) + f(n-1)，所以在计算数列中第n项的时候可用一个for循环，初始化前两项的值，计算完成第N项

之后，然后交换（n-2）项 （n-1）项的值，循环完成之后计算出的Third值即为数列中第N项的值*/

func fib(N int) int {

if N == 0 {

return 0

}

if N == 1 {

return 1

}

//f(0) = f(1), f(1) = f(2)

a, b := 0, 1

for i := 2; i <= N; i++ { //此处需要等于N

a, b = b, a+b

}

return b

}

//直接获取第几个斐波那契数--递归

func fibonacci(a int) int {

if a == 1 || a == 2 {

return 1

}

return fibonacci(a-1) + fibonacci(a-2)

}

执行结果：

D:\go\src>go run tuzi.go

21

[0 1 1 2 3 5 8 13]

21

声明：本文内容版权归原作者所有，未经授权，禁止转载！

声明：本站仅提供内容存储、展示服务，所有内容均由用户发布，不代表本站观点。请注意甄别内容中的虚假信息，谨防诈骗。如发现有害或侵权内容，可联系本站删除！